Problema MYO 311 DE SOBREGEOMETRIA

Solución de Erico Freddy Palacios Loayza

Problema MYO 310

Problema MYO 309

Problema MYO 306 de geometría

Enlace relacionado Problema MYO 305.

Solución de Erico Freddy Palacios Loayza

Solución de Rubén Darío Auqui

 Enlace relacionado

 

Problema MYO 200 de Sobregeometrias

Enlace relacionado: Problema MYO 199

Problema MYO de Sobregeometría

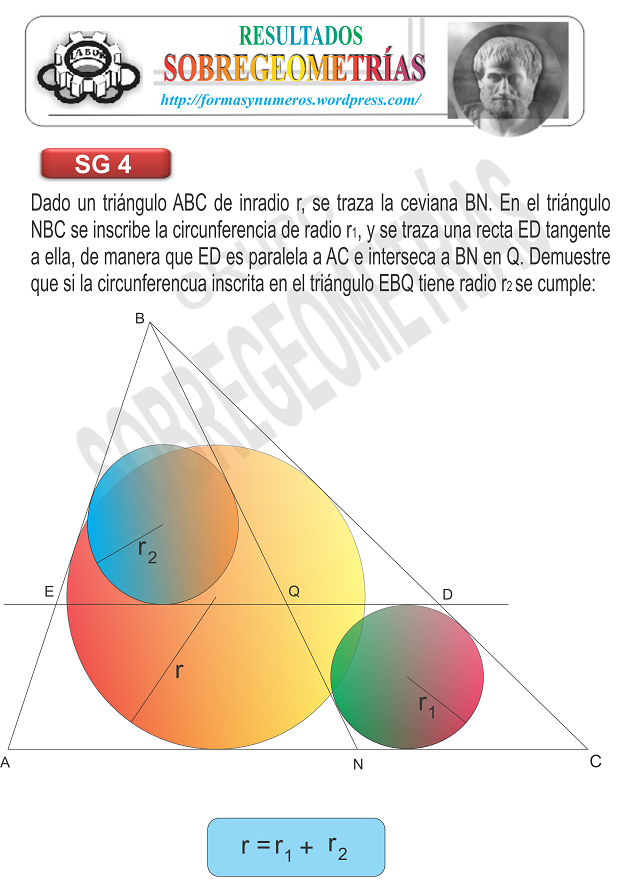
Solución por ISRAEL DIAZ
ISRAEL DIAZ:
Les he dado 4 calificativos :
a) Esbozo de Solucion : Tamaño de la Secuencia de pasos a seguir
b) Operabilidad : Dificultad con la que se completa cada paso
c) Imaginacion : Dificultad en encontrar la solucion
d) Aporte : Experiencia de propiedades y tecnicas para futura resolucion de problemas
1) Geo trigonometrica : ( largo , facil , alta , aporta mucho)http://www.facebook.com/photo.php?fbid=10151818350100385&set=a.10151670873455385.843418.894420384&type=3&theater
http://mundogeometria.files.wordpress.com/2012/06/216-1-sol.jpg
2) Geo trigonometrica : ( mediano , normal , normal , aporta poco )http://www.facebook.com/photo.php?fbid=10151818350730385&set=a.10151670873455385.843418.894420384&type=3&theater
http://mundogeometria.files.wordpress.com/2012/06/216-2-sol.jpg
3) Geometrica : ( mediano , normal , muy alta , aporta normal ))http://www.facebook.com/photo.php?fbid=10151818351260385&set=a.10151670873455385.843418.894420384&type=3&theater
http://mundogeometria.files.wordpress.com/2012/06/216-3-sol.jpg
Solución por WALTHER JAVIER BARBOZA MONTES
Un teorema previo:
http://mundogeometria.files.wordpress.com/2012/06/216-1-sol1.jpg
La Solución al problema:
http://mundogeometria.files.wordpress.com/2012/06/216-2-sol1.jpg

Problema MYO 100 : Para los que gustan de la Geometría : Sobregeometrías

Siempre me gusta resolver los problemas que se presentan en diferentes páginas amigas y una de mis preferidas en la geometría es la de Milton Donayre Peña: SobreGeometrías les dejo un interesante problema que inicialmente resolví, pero de la cual cometí un error y me salio otra respuesta.

Problema MYO 100

Desde un punto P exterior a una circunferencia se trazan las rectas tangentes PA y PB,  si M y N son puntos medios de PA y PB, respectivamente, se traza AN que intersecta a la circunferencia en S. Si la medida de ángulo MPN=36º, calcular la medida del ángulo MSN.

 

Solución de Milton Donaire

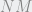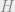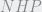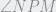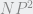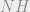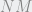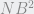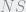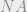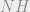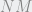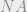Prolongamos hasta el punto de modo que , entonces = m = 36º, de allí = x y del teorema de la tangente = x, luego x = x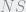 entonces el cuadrilátero 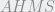es inscriptible. Como 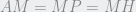, m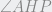 = 90º, m 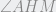= 54º de donde 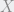= 54º.

Solución al problema MYO 6 propuesto en mundo geometría

 


Solución al problema propuesto por Milton Donaire en su web:
mundogeometria.wordpress.com SobreGeometrías

Solución al problema de mundogeometría.